这篇文章是接矩阵变换系列文章的,说明各类变换矩阵在一般用于3d图形学程序的什么阶段,如何去使用。如果还没有看过之前的矩阵变换,可以在以下地址访问:
在写一个稍微复杂的图形程序中,我们并不是一开始就是将所有的物体都放在同一个坐标系中处理的。就像设计人员在使用建模软件的时候,会将一个复杂世界中的物体单独设计,等所有东西都设计好后,在放置到同一个世界(坐标系)的不同位置,例如设计一个房间,房间内有桌子、椅子、电脑、人等等。设计师会先给房间内每一个物体建模,当设计椅子模型时,椅子所在的坐标系就是一个独立的坐标系,我们认为椅子所在的位置为这个独立坐标系的原点,同理桌子、电脑和人等其他模型也是在他们各自的坐标系中建模的。我们将这些物体单独建模的时候的这些坐标系称之为他们各自的局部坐标系。等所有模型都建好后,设计师会将这些模型移动到同一个场景中(另一个坐标系),这些模型在同一个模型中都有不同的位置,此时这个大家共同存在的场景坐标系,被称作为世界坐标系。
肯定有人要问了,为什么要这么操作,为什么不一开始就在同一个场景同时设计所有的模型,而是在不同场景设计不同的模型再放到同一场景呢?想像一下,如果工程很复杂,设计师在同一个场景,同时设计所有模型,那难度是不是增加太多,因为在同一个场景下给桌子建模的时候可能会影响到椅子模型,这大大增加了难度,而如果我们分开在不同场景设计不同的模型,模型之间互不影响,等设计好后,只需要移动到同一场景下。这样最后实现的场景是一样的,利用分而治之的思想,这大大简化了工作难度,这不是很好吗?
上面描述的过程,将不同的模型从它们所在的局部坐标系移动到同一个世界坐标系,就需要借助变换矩阵来完成了,我们将这个变换矩阵叫做模型矩阵。一般在一个图形应用中会存在以下五个坐标系和四个用于坐标系转换的矩阵:
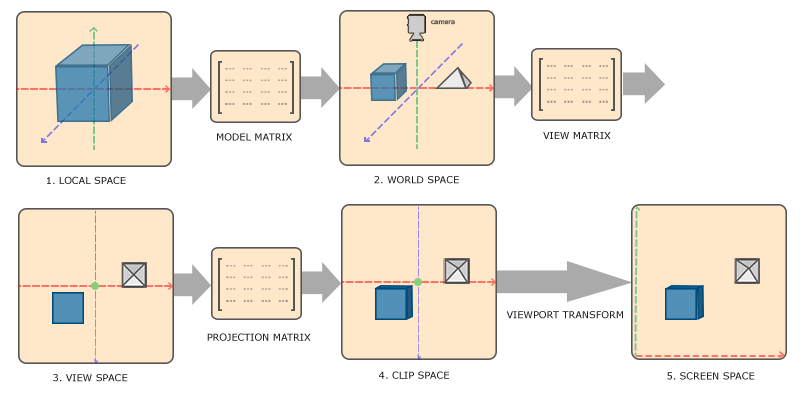
局部坐标系(局部空间):不同模型各自所在的坐标系。可以通过模型矩阵,将局部坐标转换为世界坐标。
世界坐标系(世界空间):所有模型处在同一个场景中的坐标系。通过视觉矩阵,转换为视觉坐标系。
视觉坐标系(观察空间):观察空间坐标系,用来模拟人眼(摄像机)在不同位置看向场景中某个位置,所看到的场景。坐标系原点是人(摄像机)所在的位置。
裁剪坐标系(裁剪空间/标准设备空间):坐标到达观察空间后,我们需要将其转换到裁剪空间。我们知道opengl/webgl的裁剪空间为-1~+1,所以剪裁坐标会被处理再这个范围内,并判断哪些片段将会出现在屏幕内。裁剪空间也被称为标准设备空间(NDC)。
屏幕坐标系(窗口空间):最后,我们将裁剪坐标变换为屏幕坐标,我们将使用一个叫做视口变换(Viewport Transform)的过程。视口变换将位于-1.0到1.0范围的坐标变换到由glViewport函数所定义的坐标范围内。最后变换出来的坐标将会送到光栅器,将其转化为片段。
以上所有坐标系都是三维的,可以从窗口空间逆向转换到前面的坐标系。只有标准设备空间坐标系是左手坐标系,其z轴,向屏幕外为负,向屏幕内为正。
关于坐标系统之间的转换矩阵,我在前面的矩阵变换系列的文章里都已经讲解过了。在3D图形学中的矩阵变换(一),讲解了基本的平移、旋转和缩放,可以用于构建模型矩阵, 将局部坐标转换为世界坐标。在3D图形学中的矩阵变换(二),讲解了lookAt矩阵,可以用于构建view矩阵,将世界坐标转换为观察空间坐标。在3D图形学中的矩阵变换(三)中讲解了投影矩阵,可以将观察空间变换为裁剪空间。
最后还有一个屏幕空间, 屏幕空间也是三维的,x从左向右,y从上到下,z从外到里,z的可见范围是[0, 1], 0离我们最近的近平面,1是离我们最远的远平面。知道光标位置和深度z值,可以通过逆变换得到前面任意坐标系的值,在进行物体选择的时候用得到。关于屏幕空间暂时,我不拓展开讲解,这个留到后面。
关于图形学用到的变换矩阵,你可以自己写,也可以利用一些现有的库。作为初学者目前我只用过glm和glMatrix。如果你是学opengl的,可以使用glm,如果是webgl,可以使用glMatrix。它们都是三维图形的数学库,里面提供了生成矩阵的一些函数,使用方法差不多,只是基于的语言不一样。还要其他的library,暂时没用过,也没有去了解过。可以在以下地址,获取它们。
glMatrix:https://glmatrix.net/
glm:https://glm.g-truc.net/0.9.8/index.html
本节内容旨在讲解,如何按照一定的模式去构建一个三维场景。我认为这也是学习图形学最重要的,也是最基础的一些内容吧。
我在3d俄罗斯方块中,就是用了矩阵变换思想,感兴趣的可以再下面地址中试玩,界面右上角图标可以获取源代码。
3d-tetris: https://pengfeiw.github.io/minicode/3d-tetris。
(完)。